Shoot the Pictures
I shot three pictures of my desk. I ensured to rotate about the camera axis to obtain pictures from different angles. I used pictures from the left, center, and right angles for my warping and mosaics examples below.
Desk Left
Desk Middle
Desk Right
Recover Homographies
To recover the homographies, I followed the equations below, and this basically comprised of my functions.

Warp the Images
To warp the images, I used the homography to forward warp four corners of the original image. I then found all the pixels inside the warped corners and then inverse warped them to map them to the original image. I then used interpolation to map pixels form the original image to the warped image.

Warped Room Left to the frame of Room Center
Image Rectification
For rectification, I supplied correspondances by manually clicking corners for the image as my first set of points. For the second set of points, I just used np.array([[0, 0], [400, 0], [0, 200], [400, 200]]) as my target rectification. I then computed the homography for the two sets of points. Using this homography, I warped the image using the previous step to get our rectification.
Flag

Rectified Flag

Cropped Rectified Flag
Cap

Rectified Cap

Cropped Rectified Cap
Box

Rectified Box

Cropped Rectified Box
Blend the images into a mosaic
To blend images into a mosaic, I first modified the warp function above, to provide the translation of the warped images. Using this translation, I just added the warped images on my scene and translated the next set of images, essentially adding them one-by-one to the mosaic and translating them for alignment. For the translation, I just used the top-corner of each warped image. To blend them, I used an alpha mask based on the distance from the center of an image, to get a nice blend. I then used a weight map to obtain good pixel intensities. I did this by finding the union of pixels between two images that were stitched together and then doing a weighted average on them. This is something that I might work on for 4b to improve the outputs, as it could be the result of not having a good set of pictures for a mosaic.

Mosaic
Detecting corner features in an image
I used the harris corner detector algorithm to find harris corners and overlay them on the image to verify that the points are indeed on the corners of the image. We further limit the number of harris corners using Adaptive Non Maximal Suppression (ANMS), by consolidating a group of points into a singular location and only considering new points beyond a certain radius from an existing point. This limits the computational complexity of future steps since we have less points to consider, and the points that we do have are still quite important and spread out throughout the image.
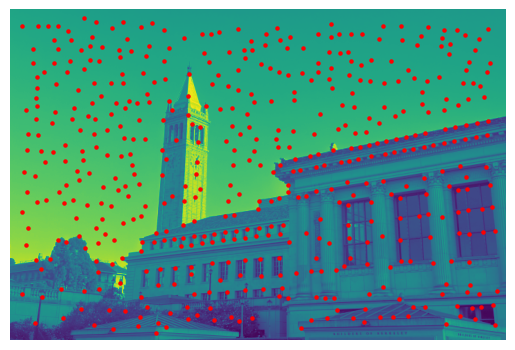
Harris Corners of Doe Library (pic1 b&w)

Harris Corners of Doe Library (pic2 b&w)
Extracting a Feature Descriptor for each feature point
I extracted feature descriptors by using a 40x40 window over a harris corner point. I then subsampled that 40x40 window into a 8x8 window which I will be using as my feature descriptors.
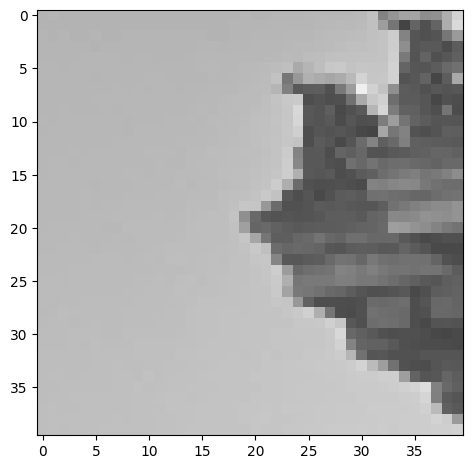
Doe Library feature window (40x40)
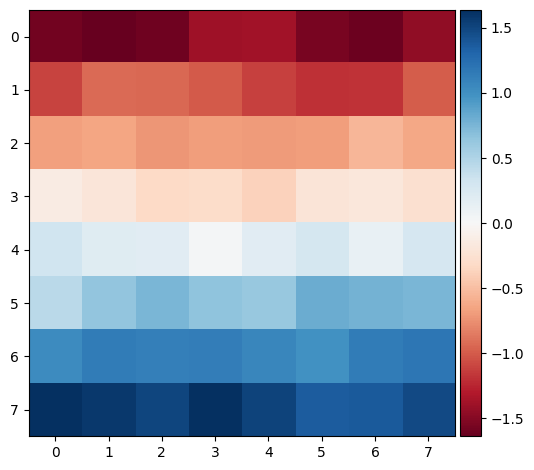
Doe Library subsampled feature (8x8)
Matching these feature descriptors between two images
Using the feature descriptors from the previous step, I found the L2 norm for every combination of feature descriptors from image 1 to image 2. I then found the first and second nearest neighbor for the norms. I then used and error threshold of 0.7 for 1-NN/2-NN to weed out features that are too different, thus only keeping the best pairs of features.

Doe Library (pic1 to pic2)

Doe Library (pic3 to pic2)
Use a robust method (RANSAC) to compute a homography
Using the feature matchings from the previous step, we then run the RANSAC algorithm. We first take a random set of 4 feature matching pairs. Then we compute a homography for those 4 points. Using this homography, we compute the distance between the original and homography transform of all the points and count the number of inliers based on a certain epsilon threshold. We do this 3-step loop for 5000+ iterations. After the 5000+ iterations, we take the largest set of inliers and compute a new Least-Squares homography on the inliers and return this new homography as our RANSAC output.
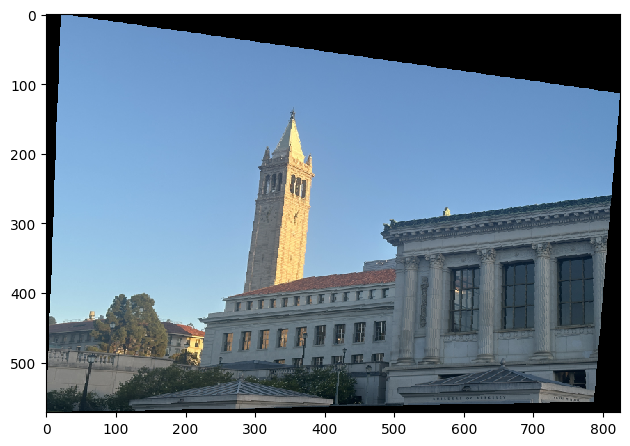
Doe (picture 1) morphed using RANSAC computed Homography
Final Mosaic with Blending
Using the RANSAC method, and the alignment and blending techniques from earlier steps, we automatically stitch together our mosaics! This process of picking correspondances is fully automated now, and we have very robust solutions. I was unable to reproduce the earlier mosaic for this step, so I have instead included 3 different examples that I computed using RANSAC.

Doe Library Mosaic

Dorm Room Desk Mosaic

International House Midnight Mosaic
What have you learned?
I learned how early digital cameras stitched together a series of photos to create panoramas! I still remeber using my dad's nokia phone to shoot panoramas, and I finally learned the algorithms behind it! I really found RANSAC to be a very useful algorithm and the nearest neighbor error threshold a very nice technique to match features. This will be very helpful in my future projects to automate a lot of correspondance choosing and image alignments.